Comprehensive Guide to Algebra Formulas for All Class Levels

Algebra Formulas are a crucial math branch in which letters replace numbers in equations. This guide offers essential algebra formulas for quick review, perfect for exam prep. It covers formulas for various class levels.
Initially, the math involved basic numbers and operations. As studies advanced, algebra introduced letters like X and Y to represent unknown values, functioning like a balanced scale where operations on one side must match the other. This guide helps you understand these concepts and provides the necessary formulas for solving algebraic equations.
What Are Algebra Formulas?
Algebra formulas are tools in math that show how different numbers or variables relate to each other. In algebra, letters stand in for unknown numbers. These formulas help us understand and solve problems by showing how these variables connect.
Introductory Algebra for Class 6
Introductory Algebra for 6th grade covers fundamental concepts. Here’s a quick look at the key terms and rules:
Key Terms:
- Exponent: Shows how many times to multiply a number by itself.
- Expression: A combination of numbers, variables, and operators (+, -).
- Polynomial: An expression of terms like monomials, binomials, and trinomials.
- Like Terms: Terms with the same variables and exponents.
- Unlike Terms: Terms with different variables or exponents.
- Constant: A fixed value that does not change.
Equation vs. Expression:
- Equation: Shows two things are equal, separated by an “=” sign.
- Expression: A group of terms joined by “+” or “-” signs but not equal to anything.
Basic Algebra Rules:
- Symmetry Rule
- Commutative Rules
- Inverse of Addition
- Two Rules for Equations
Basic Algebra Operations:
- Addition:** \( x + y \)
- Subtraction:** \( x – y \)
- Multiplication: \( x \times y \)
- Division: \( x / y \) or \( x \div y \)
Order of Operations:** Follow the BODMAS rule:
1. Brackets
2. Orders (like exponents)
3. Division and Multiplication
4. Addition and Subtraction
Basic Algebra Formulas:
| (a + b)2 | a2 + b2 + 2ab |
| (a – b)2 | a2 + b2 – 2ab |
| (a + b)(a – b) | a2 – b2 |
| (x + a)(x + b) | x2 + x(a + b) + ab |
- a2−b2=(a−b)(a+b)
- (a+b)2=a2+2ab+b2
- a2+b2=(a−b)2+2ab
- (a−b)2=a2−2ab+b2
- (a+b+c)2=a2+b2+c2+2ab+2ac+2bc
- (a−b−c)2=a2+b2+c2−2ab−2ac+2bc
- (a+b)3=a3+3a2b+3ab2+b3
- (a−b)3=a3−3a2b+3ab2−b3

Algebra Examples
Example 1: Find \( y \) when \( y + 15 = 30 \)
Solution:
y = 30 – 15
y = 15
Example 2: Find ( x \) when 9x = 63
Solution:
x = frac 63\9
x = 7
Example 3: If frac x\7 = 21, find x
Solution:
Frac x\7} = 21
x = 21 times 7
x = 147
Practice Problems:
1. Solve x + 12 = 6
2. Find the value of z if 23z + 3 = 10
3. Solve 2y – 8 = 5y
Algebra Formulas for Class 9
Logarithms help with complex multiplication and division problems. For example, the exponential expression 25=32 can be written as log 2 32=5. We can simplify these operations to addition and subtraction by converting multiplication and division into logarithms. Here are some fundamental properties of logarithms to use in these calculations.
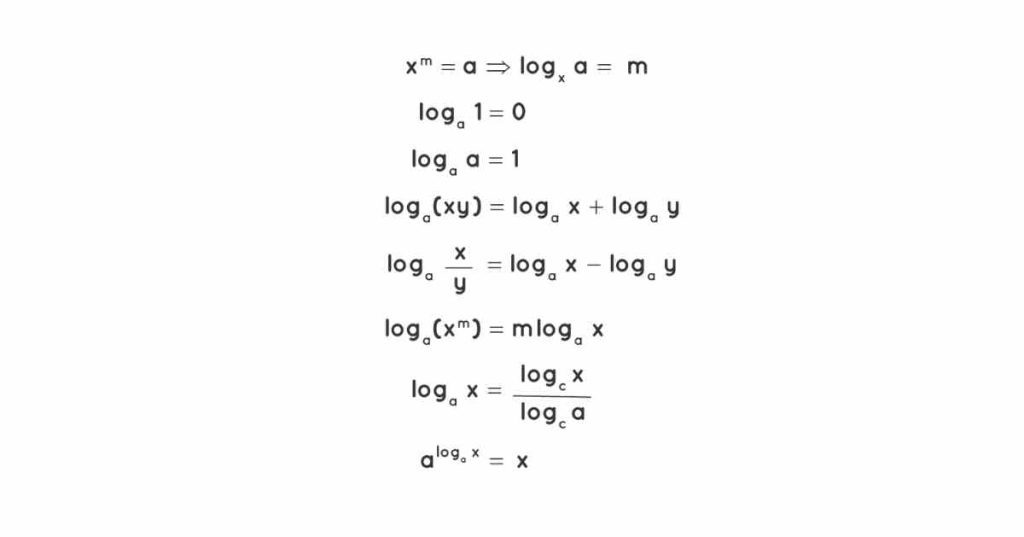
[Read More: Understanding and Applying the Tan 2x Formula in Trigonometry]
Algebra Formulas for Class 10
Square of a Binomial:
- (a+b)2=a2+2ab+b2
- (a−b)2=a2−2ab+b2(a – b)^2 = a^2 – 2ab + b^2(a−b)2=a2−2ab+b2
Product of Binomials:
- (a+b)(a−b)=a2−b2
Cube of a Binomial:
- (a+b)3=a3+3a2b+3ab2+b3
- (a−b)3=a3−3a2b+3ab2−b3(a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3(a−b)3=a3−3a2b+3ab2−b3
Sum and Difference of Cubes:
- a3+b3=(a+b)(a2−ab+b2)
- a3−b3=(a−b)(a2+ab+b2)a^3 – b^3 = (a – b)(a^2 + ab + b^2)a3−b3=(a−b)(a2+ab+b2)
Square of a Trinomial:
- (a+b+c)2=a2+b2+c2+2ab+2bc+2ca
Algebra Formulas for Class 11
1. Quadratic Equations:
- Standard Form: ax2+bx+c=0
- Quadratic Formula: x=2a−b±b2−4ac
- Roots Relationship:
- Sum of Roots: α+β=−ab
- Product of Roots: αβ=ac
2. Polynomials:
- Degree of Polynomial: Highest power of the variable
- Factor Theorem: A polynomial f(x) has a factor x−ax – ax−a if f(a)=0f(a) = 0f(a)=0
- Remainder Theorem: When f(x) is divided by x−ax – ax−a, the remainder is f(a)f(a)f(a)
3. Arithmetic Progression (AP):
- Nth Term: an=a+(n−1)d
- Sum of First \(n\) Terms: Sn=2n[2a+(n−1)d]
- Sum of \(n\) Terms (Alternative Formula):Sn=2n[a+l] where it is the last term
4. Geometric Progression (GP):
- Nth Term: an=arn−1
- Sum of First \(n\) Terms: Sn=r−1a(rn−1) for r≠1r \ne 1r=1
- Sum of Infinite GP: S=1−ra for ∣r∣<1|r| < 1∣r∣<1
5. Binomial Theorem:
- Expansion: (a+b)n=∑k=0n(kn)an−kbk
- Binomial Coefficient: (kn)=k!(n−k)!n!
6. Matrices:
- Addition and Subtraction: Perform element-wise operations
- Multiplication: ((AB)ij=∑kAikBkj
- Transpose: The transpose of matrix AAA, denoted ATA^TAT, is obtained by swapping rows and columns
Algebra Formulas for Class 12
1. Complex Numbers:
- Form: z=a+biz = a + biz=a+bi
- Modulus: ∣z∣=a2+b2|z| = \sqrt{a^2 + b^2}∣z∣=a2+b2
- Conjugate: zˉ=a−bi\bar{z} = a – bizˉ=a−bi
- Addition/Subtraction: (a+bi)±(c+di)=(a±c)+(b±d)i(a + bi) \pm (c + di) = (a \pm c) + (b \pm d)i(a+bi)±(c+di)=(a±c)+(b±d)i
- Multiplication: (a+bi)(c+di)=(ac−bd)+(ad+bc)i(a + bi)(c + di) = (ac – bd) + (ad + bc)i(a+bi)(c+di)=(ac−bd)+(ad+bc)i
- Division: a+bic+di=(a+bi)(c−di)c2+d2\frac{a + bi}{c + di} = \frac{(a + bi)(c – di)}{c^2 + d^2}c+dia+bi=c2+d2(a+bi)(c−di)
2. Matrices and Determinants:
- Matrix Addition/Subtraction: Perform element-wise operations
- Matrix Multiplication: (AB)ij=∑kAikBkj(AB)_{ij} = \sum_{k} A_{ik} B_{kj}(AB)ij=∑kAikBkj
- Transpose: (AT)ij=Aji(A^T)_{ij} = A_{ji}(AT)ij=Aji
- Determinant of 2×2 Matrix: det(A)=ad−bc\text{det}(A) = ad – bcdet(A)=ad−bc for matrix A=[abcd]A = \begin{bmatrix}a & b \\ c & d\end{bmatrix}A=[acbd]
- Inverse of 2×2 Matrix: A−1=1ad−bc[d−b−ca]A^{-1} = \frac{1}{ad – bc} \begin{bmatrix}d & -b \\ -c & a\end{bmatrix}A−1=ad−bc1[d−c−ba]
3. Sequences and Series:
Arithmetic Progression (AP):
- Nth Term: an=a+(n−1)da_n = a + (n – 1)dan=a+(n−1)d
- Sum of First nnn Terms: Sn=n2[2a+(n−1)d]S_n = \frac{n}{2} [2a + (n – 1)d]Sn=2n[2a+(n−1)d]
- Geometric Progression (GP):
- Nth Term: an=arn−1a_n = ar^{n – 1}an=arn−1
- Sum of First nnn Terms: Sn=a(rn−1)r−1S_n = \frac{a(r^n – 1)}{r – 1}Sn=r−1a(rn−1) for r≠1r \ne 1r=1
- Sum of Infinite GP: S=a1−rS = \frac{a}{1 – r}S=1−ra for ∣r∣<1|r| < 1∣r∣<1
4. Binomial Theorem:
- Expansion: (a+b)n=∑k=0n(kn)an−kbk
- Binomial Coefficient: (kn)=k!(n−k)!n!
In Summary
Understanding algebra formulas is essential for solving mathematical problems efficiently. This guide covers fundamental formulas and concepts from Class 6 to Class 12, providing a solid foundation for exam preparation. By mastering these formulas, students can simplify complex equations and excel in their math studies.






